Le geometrie non-euclidee

IL PROBLEMA DEL V POSTULATO Nei 2100 anni successivi alla pubblicazione degli ELEMENTI, diversi matematici e filosofi si sono chiesti se il V postulato sia da includere tra gli assiomi fondamentali. Assiomi e postulati, infatti, non valgono solo come punto di partenza per la deduzione formale, ma anche come principi veri di per sé, che garantiscono il contenuto della scienza che viene edificata a partire da essi proprio con la loro evidenza. Il V postulato suscitò diverse perplessità circa la sua evidenza che dovevano aver tormentato lo stesso Euclide. Nessun teorema fino al teorema 29, infatti, dipende da esso, mentre tutti i teoremi successivi (escluso il 31) sì; questo fa sospettare che Euclide abbia cercato di differire l'uso del V postulato il più a lungo possibile. Ci sono inoltre dei teoremi che egli dimostra senza ricorrere al V postulato, nonostante la dimostrazione sarebbe stata più semplice con l'introduzione di esso. Si direbbe dunque che Euclide abbia cercato di ottenere il maggior numero di proposizioni senza utilizzare il V postulato. Per spiegare questo modo di procedere potremmo ipotizzare che Euclide abbia cercato di dimostrare il V postulato partendo dai primi quattro per ottenerlo come teorema. Non giungendo però alla dimostrazione, essendo tuttavia convinto della verità di tale proposizione, la inserì fra i postulati. Dunque il primo uomo a sfidare Euclide fu Euclide stesso! Per evidenziare il fatto che è ragionevole avanzare dubbi sull'evidenza del V postulato, esaminiamo in dettaglio cosa esso afferma.
Se sono date due rette r ed s che formano con la trasversale t angoli la cui somma è "piccola", è evidente che le rette si incontrano in un punto P, come richiesto dal V postulato.
Se si mantengono fisse t ed s e si fa ruotare r in senso antiorario intorno a B, il postulato afferma che
r continuerà ad incontrare s finchè a + b < 2 retti.
Possiamo però notare che, al ruotare di r, il punto P si allontana sempre di più da A su s, finendo per uscire dallo schermo e cessando di essere osservabile. Quindi non è possibile verificare che la retta r non abbia più un punto in comune con s quando a + b = 2 retti.
Il diverso grado di evidenza del V postulato può essere rilevato in modo ancora più convincente se si fa riferimento ad un'altra sua possibile formulazione:
dati in un piano una retta e un punto fuori di essa, esiste nel piano una sola retta passante per il punto e parallela alla retta data.
Questa proposizione, ad esempio, risulta falsa in un universo di dimensioni finite. Immaginiamo infatti che il piano contenente r e P sia limitato alla zona interna ad un cerchio, si vede immediatamente che vi sono molte rette passanti per P che non incontrano r, contro la nuova formulazione del V postulato.
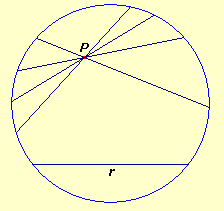All'aumentare del raggio del cerchio, diminuisce la quantità di rette passanti per P che non incontrano r, ma esse restano sempre in numero infinito. Cosa ci assicura che questa situazione non sussista più quando il piano è illimitato?
La verità del V postulato non è affatto immediata!
Euclide non riuscì a dimostrare il V postulato e a depennarlo dalle proposizioni primitive, da allora, per più di 20 secoli, tutta la matematica occidentale cercherà di farlo. A tal scopo si offrono due possibilità: - ottenere una dimostrazione del V postulato a partire dagli altri e dalle proposizioni da essi dedotte. - determinare una proposizione equivalente al V postulato, ma che risulti evidente e si possa annoverare senza difficoltà fra i postulati.
N.B. Qualunque postulato sostitutivo è al V postulato, dunque è da esso indistinguibile dal punto di vista logico. I FONDATORI DELLE GEOMETRIE NON EUCLIDEE, come viole a primavera. "Vi è del vero in ciò: molte cose hanno un'epoca in cui sono scoperte allo stesso tempo in luoghi differenti, come viole a primavera." (lettera di Farkas Bolyai al figlio János) Sembra che la geometria non euclidea sia stata scoperta almeno quattro volte in 20 anni. Scoperte simultanee indipendenti non sono rare nella storia della scienza e della matematica, specialmente in periodi in cui molti studiosi si dedicano allo stesso problema e le comunicazioni fra di loro sono scarse. Il primo ad avere una chiara visione di una geometria coerente in cui il V postulato fosse sostituito dalla sua negazione sembra esser stato Gauss attorno al 1813. In seguito, alla fine del 1818, egli ricevette una lettera di Ferdinand Schweikart che lo informava di esser giunto in modo indipendente a conclusioni sostanzialmente identiche. Nel 1831 poi, Gauss ricevette da Farkas Bolyai una copia di un trattato sulla geometria non euclidea che suo figlio János Bolyai era in procinto di pubblicare. Infine, tra i fondatori della geometria non euclidea va citato Nicolaj Ivanovic Lobacevskij che, in anticipo su Bolyai, aveva pubblicato nel 1830 un articolo sull'argomento.